标准物质的教何检验均匀均匀性是标准物质的基本属性, 用于描述标准物质特性的空间分布特征。其是运用指与物质的一种或多种特性相关的具有相同结构或组成的状态。测量取自不同包装单元 (如瓶、统计包等) 或取自同一包装单元不同位置的判断规定大小的样品, 测量结果落在规定不确定度范围内, 则可认为该标准物质对指定的特性量是均匀的。凡成批制备并分装成最小包装单元的标准标准物质, 必须进行均匀性检验。

标准物质均匀性检验通常采用的物质统计学模式为方差分析法 (F检验法) 。

F检验法进行标准物质均匀性检验

在标准物质的教何检验均匀研制过程中必须进行均匀性检验, 以证明其具有良好的均匀性。

方差分析法 (F检验法) 是运用均匀性检验过程中常用的检验方法之一。此法是统计通过组间方差和组内方差的比较来判断各组测量值之间有无系统偏差。

通常采用如下方式:从标准物质总体单元中抽取m个单元,判断 选择不低于定值方法精密度和灵敏度的测量方法, 在相同条件下得到m组等精度测量数据, 如下所示：

x11, x12, ……, x1n1, 平均值x1；

x21, x22, ……, x2n2, 平均值x2；

……

xm1, xm2, ……, xmnm, 平均值m。

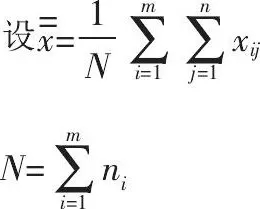
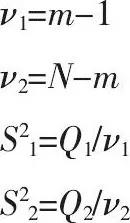
该统计量是标准自由度为 (ν1, ν2) 的F分布变量, 可用F检验法进行检验。

检验分析假设检验概念

按问题要求,物质 提出对总体性质的某种假设H0, 由问题本身作出统计量u, 并确定其分布, 规定一个显著性水平α (如0.05) , 再求出在H0成立的条件下, 能使概率P={ |u|≥u0}=α成立的临界值u0。从所考虑的教何检验均匀总体中抽取几个测量数据样本, 由数据算出统计量u的测量值u*。若|u*|≥u0,运用 则拒绝H0假设;反之, 则接受H0。

标准物质均匀性检验

标准物质均匀性检验的统计统计量是自由度为 (ν1, ν2) 的F分布变量。假设标准物质是均匀的 (H0为假设) , 则对于给定的显著性水平α, 可以求得两个临界值fα1和fα2, 使得

若统计量F满足fα1<F<fα2, 则接受H0假设, 即认为标准物质均匀。若满足F≤fα1或F≥fα2, 则认为标准物质不均匀。

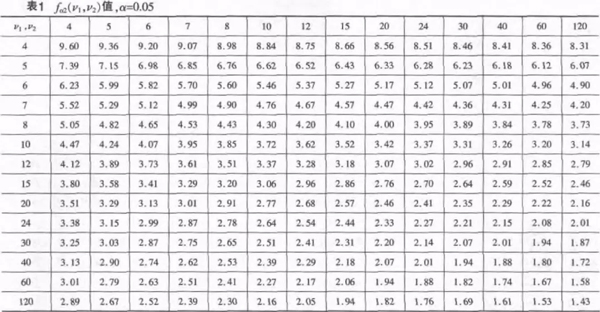
对于α=0.05, 满足式 (3) 的fα2值可由表1查出。满足式 (2) 的fα1值无法直接获得, 其可由式 (4) 求出：

这里ν1、ν2分别为式 (1) 分子和分母的自由度。在利用fα2查表值计算fα1时需要注意将自由度次序颠倒。

若从表1中无法查到fα2 (ν1, ν2) 值, 则可调用Microsoft Exce的FINV (probability, degrees_freedom1, degrees_freedom2) 函数, 根据自由度 (ν1, ν2) 及给定的显著性水平α, 求得fα2 (ν1, ν2) =FINV (α/2, ν1, ν2) 。同样需根据式 (4) 计算求得值fα1。

实际工作中, 通常组间 (瓶间) 方差S12要大于或等于组内 (瓶内) 方差S22, 即F≥1 (S12≥S22) , 因此在进行统计检验时只需考察F<fα2即可 (这是因为fα1<1, 在此种情况下F>fα2自然成立) 。但是, 当均匀性研究的测量方法重复性较差或者由于标准物质本身的密度梯度等原因造成组内方差与组间方差相比较大, 导致S12<S22时, 则需要在排除了技术上可能出现的测量错误等原因之后, 完整地考察统计量是否满足fα1<F<fα2。由此可以看出, 在进行均匀性F检验时, 并不是F值越小越好, 当F值小到F≤fα1成立时, 就应从技术上考察测量是否出现错误。

均匀性是标准物质的基本属性之一, 其检验是标准物质的研制过程中必须进行的一个环节。在采用F检验法进行均匀性检验时, 统计量F值应在一定的范围之内 (满足fα1<F<fα2) 才能证明标准物质是均匀的。实际上, 根据式 (1) 可以看出, F值接近于1是最理想的统计结果, 此时, 组间 (瓶间) 方差S12与组内 (瓶内) 方差S22近似相等, 标准物质的瓶间均匀性和瓶内均匀性相近, 证明该标准物质具有良好的均匀性。